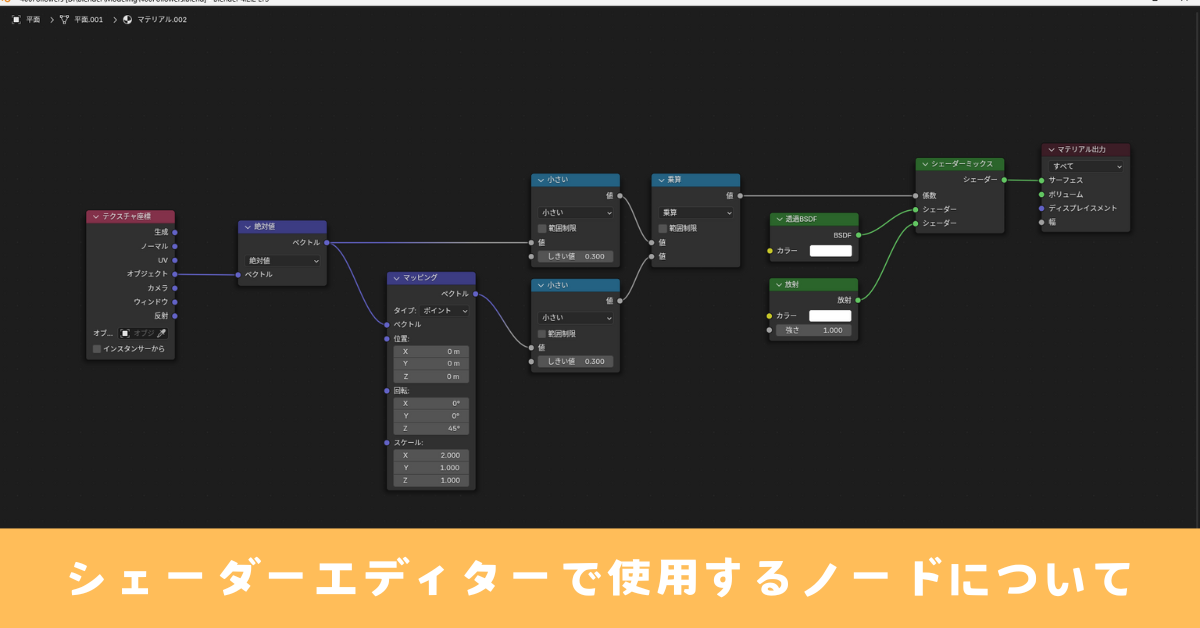
私が使用したノードの中で理解した内容のみ更新していきます。
簡略的ではなくなるべく詳細に記載していこうと考えていますので記事の1つ1つの項目が長くなるかもしれませんがご了承ください。
なるべくノード別で記載しますので目次を活用して必要な情報へアクセスしてください。
入力(Input)
テクスチャ座標(Texture Coordinate)
オブジェクト(Object)
テクスチャ座標のオブジェクトをマテリアル出力に接続した結果が下記の動画になります。
オブジェクトをマテリアル出力に接続するとなぜこの配色になるのかを理解するには下記の内容を理解する必要があります。
- 原点の位置
- オブジェクト出力と色の関係
- 座標値の正規化
原点の位置
原点の座標を基準に反映される色が決まっていきます。
原点の座標がなぜ大事なのかは後半の説明にある正規化の話で分かると思います。
原点と色が関係しているを視覚的に知る方法は下記の動画を参照してください。
<やり方>
1.3Dビューポートの右上にあるオプション内の原点にチェックを入れます
2.対象のオブジェクトを選択し、Gキーで原点を移動
動画のように原点を移動させると配色も変化することがわかると思います。
ここで一番大事なのは原点の位置を基準としたXYZ値になります。
原点の値を0とした時、XYZ値は以下のようになります。
- X軸:原点より左は負の値、右は正の値
- Y軸:原点より手前は負の値、奥は正の値
- Z軸:原点より下は負の値、上は正の値
3Dビューポートの右上に表示されているギズモからも正負の確認を行うことができます。
今は「へぇー、そうなんだ」程度で大丈夫です。
オブジェクト出力と色の関係
オブジェクト出力は、オブジェクト上の各点のX、Y、Z座標点を出力します。
カラー情報はR(赤)、G(緑)、B(青)の値で表され、座標と色の関係は下記のようになります。
- X座標:赤(R)
- Y座標:緑(G)
- Z座標:青(B)
これはBlender内全般同じ認識です。
座標値の正規化
<正規化とは>
時間で考えると簡単にイメージできるかもしれません。
例えば、
「A点からB点までは60秒かかり、B点からC点までは2分かかりました。合計何分かかりましたか?」
という問題があった時、秒を分に直し、2つの時間を足して答えを求めると思います。
この異なる基準や単位を持つ値を共通の基準に合わせる行為が正規化するということになります。
では、座標値の正規化とは何をしているかの話に戻ります。
まず、Blenderで使用する色の値とテクスチャ座標から出力される値は異なる値となっています。
詳細は下記になります。
- Blenderでの色の値:0~1の範囲
- テクスチャ座標の値:-1~1の範囲
テクスチャ座標の値をBlenderの基準に正規化する時には下記のような式が使われます。
(座標値×0.5)+0.5=正規化された値
この式を使ってRGB座標を算出すると立方体の配色の説明ができます。
立方体を正面から見たときの色は画像のようになっています。
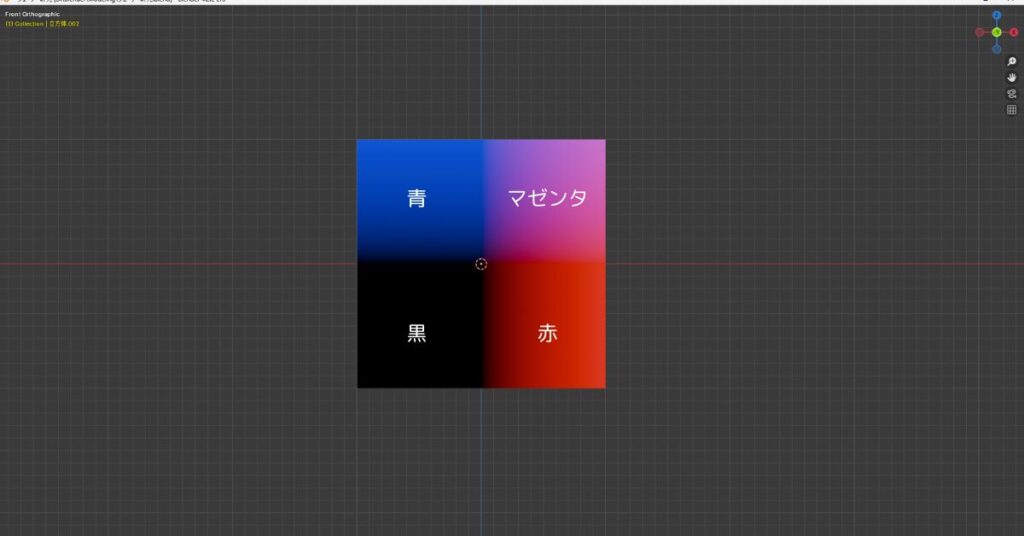
画像は正面図になるので、原点から見て右、上、奥が正の値となります。
正と負の位置関係を認識出来たら、今度はテクスチャ座標の値を考えます。
- X軸:右の辺が+1で左の辺が-1
- Y軸:手前の面が-1で奥の面が+1
- Z軸:上の辺が+1で下の辺が-1
これらを踏まえて式に代入すると青の場合
- X軸:(-1×0.5)+0.5=0
- Y軸:(-1×0.5)+0.5=0
- Z軸:(+1×0.5)+0.5=1
となります。
各軸の色成分に当てはめると
- 赤(X軸):0
- 緑(Y軸):0
- 青(Z軸):1
となるので左上の配色は青になるということです。
厳密には左に向かうほど青になるという言い方が正しいですね。
正規化した値を確認したい場合は、シェーダーのコンバーター内にあるXYZ合成または、カラー合成をマテリアル出力に接続して確認してみてください。
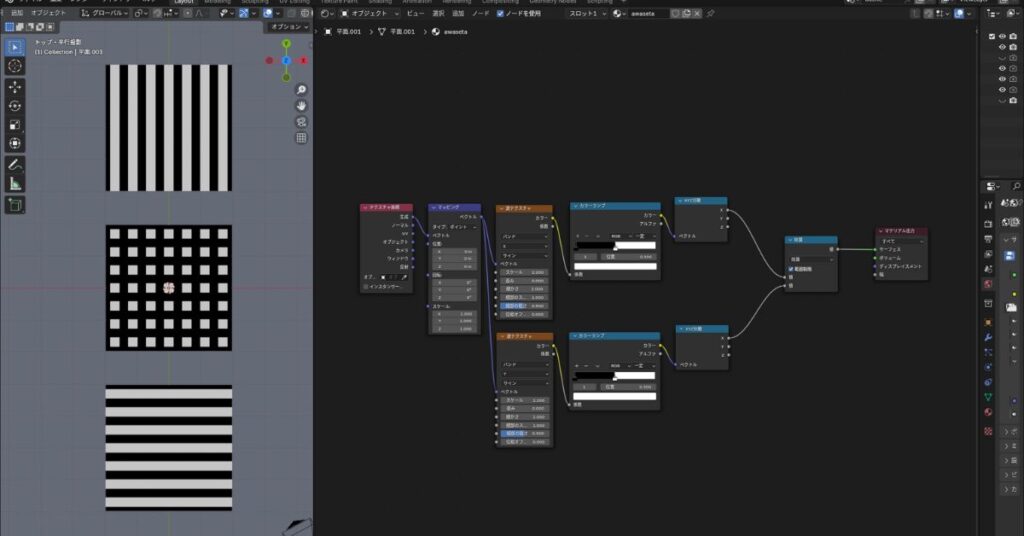
コンバーター(Converter)
数式(Math)
加算・減算・乗算についてはわかりやすい説明をしていた下記の動画の説明を引用させてもらってます。
※黒は0、白は1という概念を持って読んでください。
また、共通機能のClampについても説明します。
範囲制限(Clamp)とは
数式ノード(Math)の出力値を0~1の範囲に制限する機能です。
無効/有効それぞれの計算結果については下記を参照してください。
- 0 + 0 = 0
- 1 + 0 = 1
- 1 + 1 = 2
- 0 – 1 = -1
- 0 + 0 = 0
- 1 + 0 = 1
- 1 + 1 = 1
- 0 – 1 = 0
というような感じで無効の場合は通常の数式計算のままですが、有効の場合は0以下は0に1以上は1に制限されます。
視覚的に試したい場合は、加算(Add)の具体例で試してみるとわかりやすいと思います。
どんな時に有効にするのか
シェーダー内での計算結果が予期せず極端な値(非常に大きい値や負の値)になるのを防ぎたい時に有効にしましょう!
加算(Add)
役割
入力Aと入力Bの値を加算した結果を出力します。
式:A + B
具体例
縦縞と横縞のテクスチャを加算した場合で説明します。
画像の左側にある真ん中のテクスチャが加算結果になります。
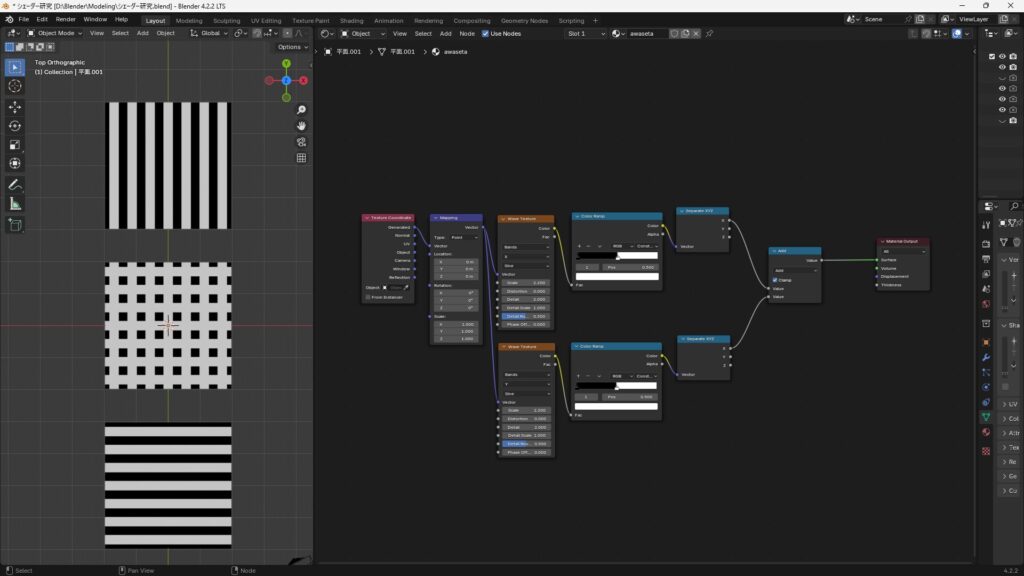
なぜ、このような結果になるかというと
- 0(黒)+ 0(黒)= 0(黒)
- 1(白)+ 0(黒)= 1(白)
- 0(黒)+ 1(白)= 1(白)
- 1(白)+ 1(白)= 1(白)
縦縞と横縞の白と黒それぞれ重なった部分で上記の計算が行われ、その結果として白が基調の網目模様になっています。
0(黒)+ 0(黒)= 0(黒)の組み合わせ以外白になるというのも特徴ですね。
Clampが無効になっている場合は、1(白)+ 1(白)= 2(白)となるので、周りの白よりも明るい白で表示されます。
減算(Subtract)
役割
入力Aの値から入力Bの値を減算した結果を出力します。
式:A – B
具体例
縦縞と横縞のテクスチャを減算した場合で説明します。
画像の左側にある真ん中のテクスチャが減算結果になります。
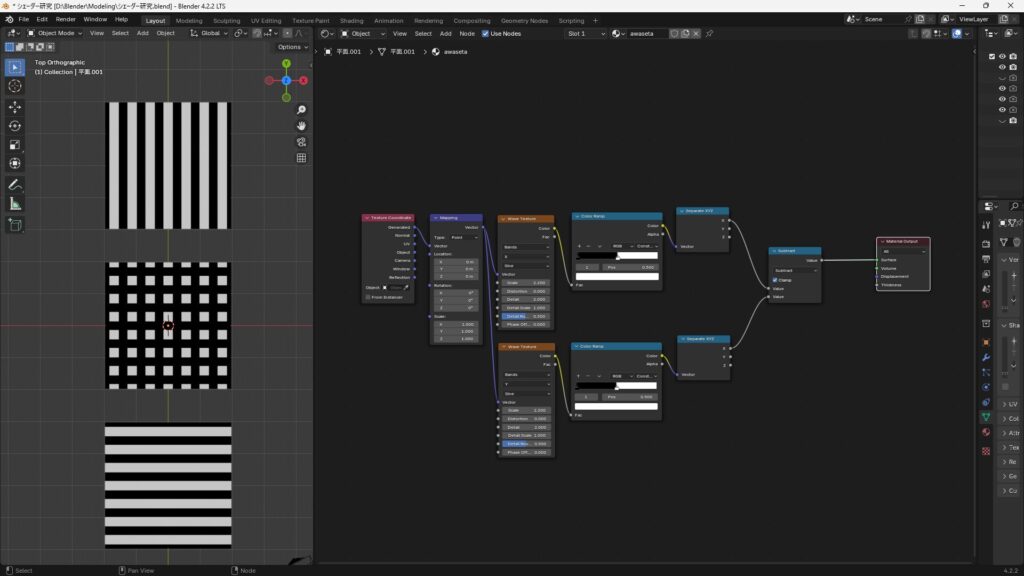
なぜ、このような結果になるかというと
- 0(黒)- 0(黒)= 0(黒)
- 1(白)- 0(黒)= 1(白)
- 0(黒)- 1(白)= 0(黒)
- 1(白)- 1(白)= 0(黒)
縦縞と横縞の白と黒それぞれ重なった部分で上記の計算が行われ、その結果として黒が基調の網目模様になっています。
1(白)- 0(黒)= 1(白)の組み合わせ以外黒になるというのも特徴ですね。
Clampが無効になっている場合は、0(黒)- 1(白)= -1(黒)となるので、計算上周りの黒よりも暗い黒で表示されるはずですが視覚的には変化を感じないと思います。
乗算(Multiply)
役割
入力Aと入力Bの値を掛け合わた結果を出力します。
式:A * B
具体例
縦縞と横縞のテクスチャを乗算した場合で説明します。
画像の左側にある真ん中のテクスチャが乗算結果になります。
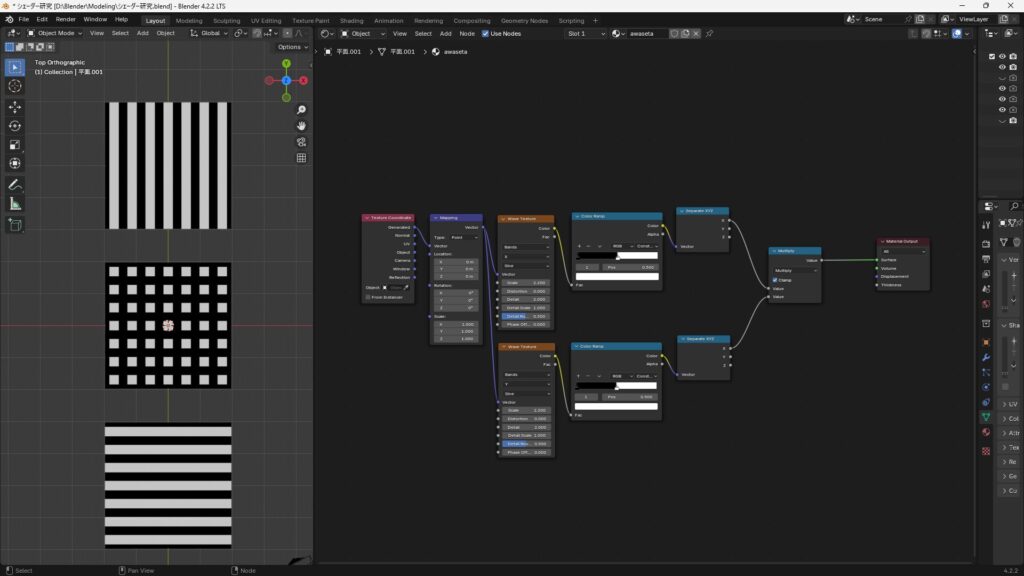
なぜ、このような結果になるかというと
- 0(黒)* 0(黒)= 0(黒)
- 1(白)* 0(黒)= 0(黒)
- 0(黒)* 1(白)= 0(黒)
- 1(白)* 1(白)=1(白)
縦縞と横縞の白と黒それぞれ重なった部分で上記の計算が行われ、その結果として黒が基調の網目模様になっています。
1(白)* 1(白)=1(白)の組み合わせ以外黒になるというのも特徴ですね。
また、Subtractと似ていますが、出力結果としては微妙に差があるので注意しましょう。
除算(Divide)
役割
入力Aと入力Bの値を割った結果を出力します。
式:A / B
具体例
縦縞と横縞のテクスチャを除算した場合で説明します。
画像の左側にある真ん中のテクスチャが除算結果になります。
なぜ、このような結果になるかというと
- 0(黒)/ 0(黒)= 0(黒)
- 1(白)/ 0(黒)= 0(黒)
- 0(黒)/ 1(白)= 0(黒)
- 1(白)/ 1(白)=1(白)
縦縞と横縞の白と黒それぞれ重なった部分で上記の計算が行われ、その結果として黒が基調の網目模様になっています。
1(白)* 1(白)=1(白)の組み合わせ以外黒になるというのも特徴ですね。
また、出力結果は乗算と同じ結果となります。
積和算(Multiply Add)
役割
入力Aと入力Bを掛けた後、その結果と入力Cの値を加算する。
式:A * B + C
要は前述で説明している加算と乗算を組み合わせたノードということになります。
具体例
縞模様とノイズテクスチャを使用して説明します。
各テクスチャを下記のように接続します。
- 入力A:波テクスチャ(X)
- 入力B:波テクスチャ(Y)
- 入力C:ノイズテクスチャ
接続した結果が以下の画像のようになります。
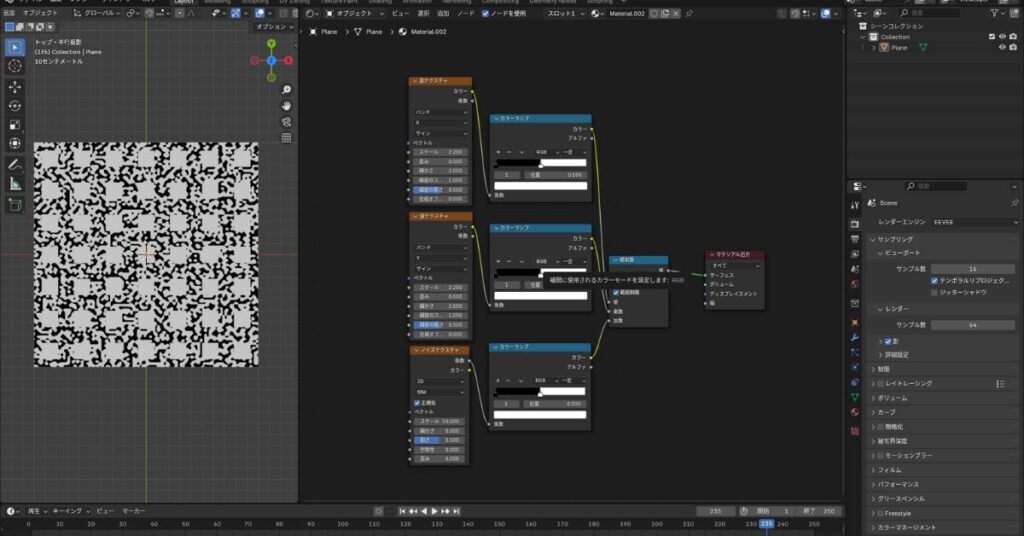
なぜこのような結果になるか考えるときは分解して考えましょう。
まず、乗算を行います。
内容としては乗算の項目で説明した内容と同じなので式だけ記載してそれ以外の説明は割愛します。
- 0(黒)* 0(黒)= 0(黒)
- 1(白)* 0(黒)= 0(黒)
- 0(黒)* 1(白)= 0(黒)
- 1(白)* 1(白)=1(白)
結果として下記の画像のような結果となるんでしたね。

では次に、加算を行っていきます。
上記の乗算の結果にのノイズテクスチャを加算すると説明の最初に載せた画像のような出力結果となります。
一応組み合わせがわかりやすい画像を下記に載せておきます。
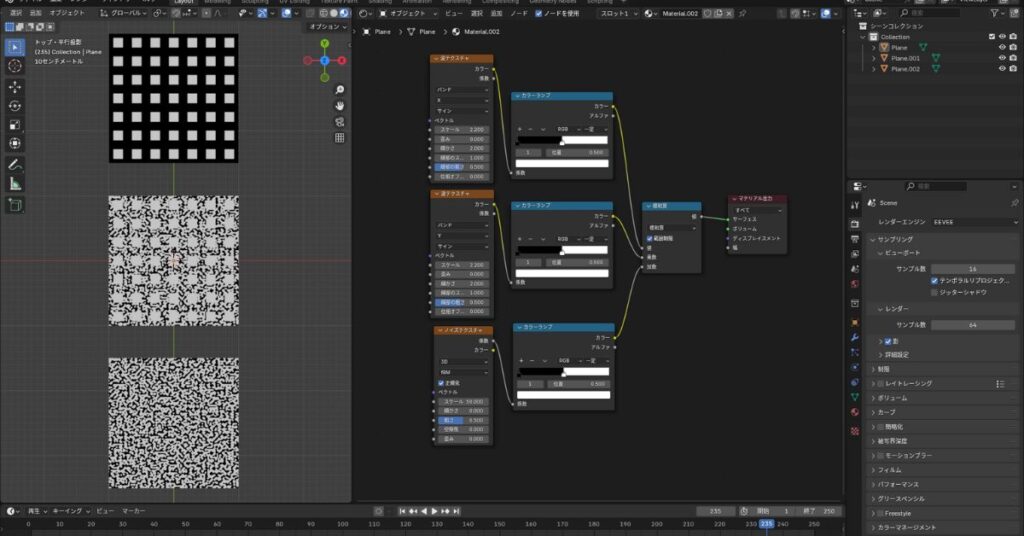
加算の式は以下になります。
- 0(黒)+ 0(黒)= 0(黒)
- 1(白)+ 0(黒)= 1(白)
- 0(黒)+ 1(白)= 1(白)
- 1(白)+ 1(白)= 1(白)
式からもわかるように波テクスチャの乗算した結果の黒い部分にのみノイズテクスチャの白い部分の影響を反映して上記のような出力になるというわけです。
累乗(Power)
役割
入力Aを入力B乗した値を出力する。
式:AB
具体例
まず、わかりやすいように数字で説明します。
数式ノードのベース(入力A)に2、指数(入力B)に3が入力されていた場合
「23」となり、これを計算すると「2 * 2 * 2 = 8」となるので
数式ノード(累乗)から出力される値は「8」になるということです。
では、次に縦縞と横縞の組み合わせの出力で考えてみましょう。
最初に出力結果を見てみます。
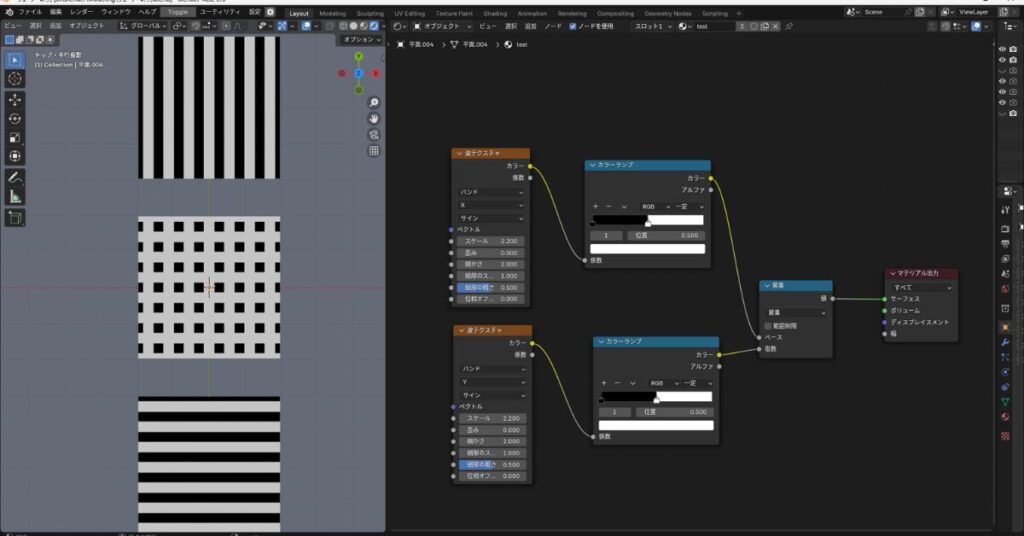
縦縞がそのまま出力されると思っていたので、この出力結果が予想外でした。
その理由は以下の計算式と出力になると考えていたからです。
- 00 = 0(黒)
- 01 = 0(黒)
- 10 = 1 (白)
- 11 = 1(白)
要は、縦縞の黒い部分の出力結果は黒で、白い部分の出力結果は白になると思ったというわけです。
累乗について理解を深めたい方は以下のサイトの説明がわかりやすかったので見てみてください。
しかし、現実の出力結果としては白を基調とした格子模様が出力されました。
なぜ格子模様が出力されたのか?
これは、「00 = 0(黒)」の式の計算結果が違うからです。
上記のサイト内でも説明されていますが、「00 = 0(黒)」は存在しません。
つまり、未定義ということになります。
では、Blender内ではどのように扱われているかというと以下のようになります。
- 00 = 1(白)
これに関してはそういうものって感じで覚えるしかないですね。
視覚的に確認したい方は以下の動画のように試してみてください。
以上のことから白を基調とした格子模様が出力されるということになります。
Log(Logarithm)
役割
入力A(値)の値は入力B(ベース)の何乗かを出力する。
式:LogB A
具体例
例えば、「Log2 8」という式だとします。
この場合、「2」が入力Bで「8」が入力Aなので前述の役割での説明の文章に当てはめると「8は2の何乗か」その答えを出力するということになります。
なので、Logから出力される値は「3」ということになります。
※この項目を更新したタイミングでは視覚的な例をうまく作れなかったので今後わかりやすい物ができ次第更新します。
より小さい(Less Than)
役割
入力Aの値が入力Bの値より小さいかどうかを判断します。
- 条件が真(入力A < 入力B)の場合:1を出力
- 条件が偽(入力A >= 入力B)の場合:0を出力
具体例
模様無しと縦縞で説明します。
まず、単純な模様が無い状態で動きを確認しましょう。
事前準備として数式ノードをより小さい・しきい値を0.8に設定しましょう。
役割で説明した内容と照らし合わせると、0.79以下が白、0.80以上が黒で出力されるはずです。
実際に値を入力して確認した結果が以下の動画になります。
言っていた通りの結果となりましたね。